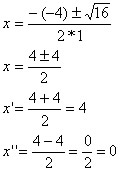Clube da Matemática
O seu segundo professor de matemática
Visualizações
quinta-feira, 7 de novembro de 2013
sábado, 14 de setembro de 2013
Fatoração Algébrica.
* Definição: Fatorar um número significa representa-lo pela multiplicação de dois ou mais fatores que são divisores do número em questão.
Ex: 45> 3x15/ 5x9/ 45x1 .
*Note que: 2a + a.
2.a + a.
> Fator comum: a.
a(2+1)> Fatoração;
Ex= Az + Bz + Cz
> Fator comum: z
z(a + b + c).
Exercício Resolvido
1- Calcule:
a) 10x (Elevado a 3) + 5x (Elevado a 2) - 25x = 5x.( 2x "ELEVADO A 2" + X - 5).
Explicação de Luíz Carlos.
Professor de Matemática do CBB.
Salvador-BA
2013
Ex: 45> 3x15/ 5x9/ 45x1 .
*Note que: 2a + a.
2.a + a.
> Fator comum: a.
a(2+1)> Fatoração;
Ex= Az + Bz + Cz
> Fator comum: z
z(a + b + c).
Exercício Resolvido
1- Calcule:
a) 10x (Elevado a 3) + 5x (Elevado a 2) - 25x = 5x.( 2x "ELEVADO A 2" + X - 5).
Explicação de Luíz Carlos.
Professor de Matemática do CBB.
Salvador-BA
2013
quarta-feira, 4 de setembro de 2013
Curiosidade!!
* COMO SE MULTIPLICA NA CHINA??
By: Equipe Polimática.
Feito por: Júlio César e Davi Garrido.
By: Equipe Polimática.
Feito por: Júlio César e Davi Garrido.
Curiosidade!!
* COMO SURGIU A MATEMÁTICA?

Os números nem sempre estiveram presentes na vida do homem. Foram nossos antepassados que começaram a criar símbolos que representavamquantidade há bastante tempo atrás. Um exemplo: existem registros de números com mais de 27 mil anos na África
No ano 3000 antes de Cristo, os povos egípcios e babilônios já tinham sistemas numéricos e até livros para ensinar os cálculos. Com a ajuda de alguns filósofos da antiga Grécia – como Tales e Pitágoras – no século 6 antes de Cristo, a matemática começou a ficar parecida com o que conhecemos hoje. Depois de um longo processo de desenvolvimento, essa ciência começou a fazer parte do cotidiano de todos nós!
By: Equipe Polimática.
Feito por: Júlio César e Davi Garrido.

Os números nem sempre estiveram presentes na vida do homem. Foram nossos antepassados que começaram a criar símbolos que representavam
No ano 3000 antes de Cristo, os povos egípcios e babilônios já tinham sistemas numéricos e até livros para ensinar os cálculos. Com a ajuda de alguns filósofos da antiga Grécia – como Tales e Pitágoras – no século 6 antes de Cristo, a matemática começou a ficar parecida com o que conhecemos hoje. Depois de um longo processo de desenvolvimento, essa ciência começou a fazer parte do cotidiano de todos nós!
By: Equipe Polimática.
Feito por: Júlio César e Davi Garrido.
domingo, 1 de setembro de 2013
Para reforçar!!!
Produtos Notáveis Parte 1
Produtos Notáveis Parte 2.
Para melhor aprendizado!!
By: Equipe Polimática.
Postador: Davi Garrido.
Curiosidade: Diferença em conceito de Matemática e Matemático!!
* Matemática:
A palavra "Matemática" tem origem na palavra grega "máthema" que significa Ciência, conhecimento ou aprendizagem, derivando daí "mathematikós", que significa o prazer de aprender.
É comum definir a Matemática como o estudo de tópicos como quantidades, formas, espaço e mudança, através do método dedutivo, no qual se pressupõe um conjunto de axiomas e regras de inferência como forma de obter propriedades das entidades em estudo.
*Matemático:
Matemático é um ser ativo na matemática, que estuda a matemática e encara os desafios com lógica e precisão sendo exato em suas contas, sendo rolutos como professores.
By: Equipe Polimática.
Postador: Davi Garrido.
A palavra "Matemática" tem origem na palavra grega "máthema" que significa Ciência, conhecimento ou aprendizagem, derivando daí "mathematikós", que significa o prazer de aprender.
É comum definir a Matemática como o estudo de tópicos como quantidades, formas, espaço e mudança, através do método dedutivo, no qual se pressupõe um conjunto de axiomas e regras de inferência como forma de obter propriedades das entidades em estudo.
*Matemático:
Matemático é um ser ativo na matemática, que estuda a matemática e encara os desafios com lógica e precisão sendo exato em suas contas, sendo rolutos como professores.
By: Equipe Polimática.
Postador: Davi Garrido.
quinta-feira, 29 de agosto de 2013
Produtos Notáveis
Considerações iniciais
Os gregos, na antiguidade, faziam uso de procedimentos algébricos e geométricos exatamente iguais aos produtos notáveis modernos. É importante destacar que o uso de sua maioria foi atribuído aos pitagóricos e estão registrados na obra de Euclides de Alexandria Elementos na forma de representações geométricas.
Verifiquem a representação e utilização da propriedade da potenciação em seu desenvolvimento.
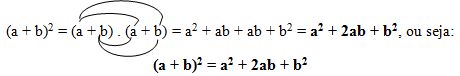
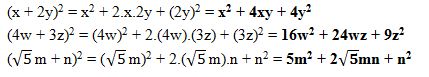
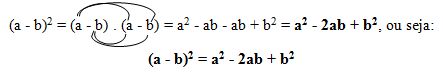
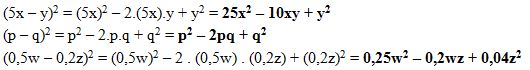
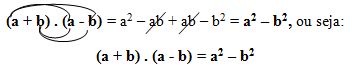
Os conceitos sobre os produtos notáveis merecem muita atenção, pois seu uso facilita cálculos, reduz o tempo de resolução e agiliza o aprendizado. O conhecimento dessa ferramenta não implica dizer que não necessitamos saber o desenvolvimento do cálculo proposto, apenas que temos mais caminhos convergentes à solução final. Utilizamos o termo notável para apontar sua importância, sua notabilidade e sua carência de atenção.
Ao lidarmos com operações algébricas, perceberemos que alguns polinômios aparecem frequentemente e, ainda, exibem certa regularidade. Esses são os produtos notáveis. Aqui estudaremos o quadrado da soma de dois termos, oquadrado da diferença de dois termos, o produto da soma pela diferença de dois temos, o cubo da soma de dois termos e, por fim, o cubo da diferença de dois termos. Vamos à explanação de cada um deles.
1. O quadrado da soma de dois termos
(a + b)2 = (a + b) . (a + b)
Onde a é o primeiro termo e b é o segundo.
Ao desenvolvermos esse produto, utilizando a propriedade distributiva da multiplicação, teremos:
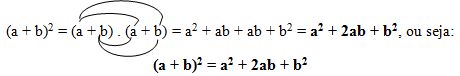
O quadrado da soma de dois termos é igual ao quadrado do primeiro termo, mais duas vezes o produto do primeiro termo pelo segundo, mais o quadrado do segundo termo.
Exemplos
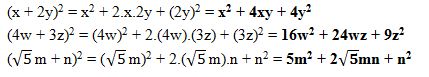
2. O quadrado da diferença de dois termos
Seguindo o critério do item anterior, temos:
(a – b)2 = (a – b) . (a – b)
Onde a é o primeiro termo e b é o segundo.
Ao desenvolvermos esse produto, utilizando a propriedade distributiva da multiplicação, teremos:
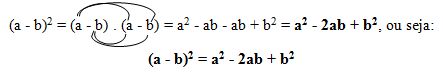
O quadrado da diferença de dois termos é igual ao quadrado do primeiro termo, menos duas vezes o produto do primeiro termo pelo segundo, mais o quadrado do segundo termo.
Exemplos:
Exemplos:
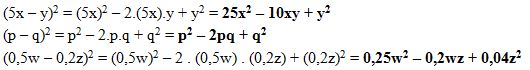
3. O produto da soma pela diferença de dois termos
Se tivermos o produto da soma pela diferença de dois termos, poderemos transformá-lo numa diferença de quadrados.
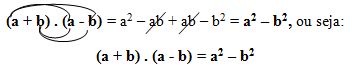
O produto da soma pela diferença de dois termos é igual ao quadrado do primeiro termo, menos o quadrado do segundo termo.
Exemplos
- (4c + 3d).(4c – 3d) = (4c)2 – (3d)2 = 16c2 – 9d2
- (x/2 + y).(x/2 – y) = (x/2)2 – y2 = x2/4 – y2
- (m + n).(m – n) = m2 – n2
4. O cubo da soma de dois termos
Consideremos o caso a seguir:
(a + b)3 = (a + b).(a + b)2 → potência de mesma base.
(a + b).(a2 + 2ab + b2) → (a + b)2
Aplicando a propriedade distributiva como nos casos anteriores, teremos:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
O cubo da soma de dois termos é igual ao cubo do primeiro termo, mais três vezes o produto do quadrado do primeiro termo pelo segundo, mais três vezes o produto do primeiro termo pelo quadrado do segundo, mais o cubo do segundo termo.
Exemplos:
- (2x + 2y)3 = (2x)3 + 3.(2x)2.(2y) + 3.(2x).(2y)2 + (2y)3 = 8x3 + 24x2y + 24xy2 + 8y3
- (w + 3z)3 = w3 + 3.(w2).(3z) + 3.w.(3z)2 + (3z)3 = w3 + 9w2z + 27wz2 + 27z3
- (m + n)3 = m3 + 3m2n + 3mn2 + n3
5. O cubo da diferença de dois termos
Acompanhem o caso seguinte:
(a – b)3 = (a – b).(a – b)2 → potência de mesma base.
(a – b).(a2 – 2ab + b2) → (a – b)2
Aplicando a propriedade distributiva como nos casos anteriores, teremos:
(a – b)3 = a3 – 3a2b + 3ab2 – b3
O cubo da diferença de dois termos é igual ao cubo do primeiro termo, menos três vezes o produto do quadrado do primeiro termo pelo segundo, mais três vezes o produto do primeiro termo pelo quadrado do segundo, menos o cubo do segundo termo.
Exemplos
- (2 – y)3 = 23 – 3.(22).y + 3.2.y2 – y3 = 8 – 12y + 6y2 – y3 ou y3– 6y2 + 12y – 8
- (2w – z)3 = (2w)3 – 3.(2w)2.z + 3.(2w).z2 – z3 = 8w3 – 12w2z + 6wz2 – z3
- (c – d)3 = c3 – 3c2d + 3cd2 – d3
Considerações finais
Utilizando os produtos notáveis, certamente aceleraremos o cálculo, permitindo o progresso em temas posteriores da matemática. A propriedade distributiva da multiplicação foi determinante para se chegar ao desenvolvimento dos produtos levando-os a sua fase reduzida. Jamais deveremos deixar de buscar conhecimentos mais profundos, como demonstrações de teoremas a fim de compreendermos melhor os caminhos trilhados para se chegar às pequenas fórmulas, tão úteis, como as conhecemos hoje.
domingo, 18 de agosto de 2013
Polígonos (Introdução).
Polígonos são figuras fechadas formadas por segmentos de reta, sendo caracterizados pelos seguintes elementos: ângulos, vértices, diagonais e lados. De acordo com o número de lados a figura é nomeada.
Classificação dos polígonos:
Lados/Nomes
3: Triângulo
4: Quadrilátero
5: Pentágono
6: Hexágono
7: Heptágono
8: Octógono
9: Eneágono
10: Decágono
11: Hendecágono ou Undecágono
12: Dodecágono
Polígonos convexos e não convexos:
Se os ângulos do polígono forem menores que 180º ele será convexo.

Caso tenha um ângulo com medida maior que 180º ele será classificado como não convexo ou côncavo.

Ângulos de um polígono:
A soma dos ângulos internos de qualquer polígono depende do número de lados (n), sendo usada a seguinte expressão para o cálculo: S = (n – 2)*180, onde n o número de lados.
A soma dos ângulos externos de qualquer polígono sempre será 360º, baseando-se no seguinte princípio: quanto maior o número de lados do polígono mais ele se assemelha a uma circunferência (possui giro completo igual a 360º).

Polígono regular e irregular:
Todo polígono regular possui os lados e os ângulos com medidas iguais. Alguns exemplos de polígonos regulares.
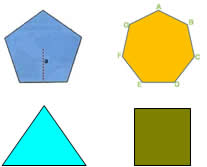
Um polígono irregular é aquele que não possui os ângulos com medidas iguais e os lados não possuem o mesmo tamanho.

Diagonais de um polígono:
Diagonal de um polígono é o segmento de reta que liga um vértice ao outro, passando pelo interior da figura. O número de diagonais de um polígono depende do número de lados (n) e pode ser calculado pela expressão:
.jpg)
By: Davi Garrido (Postador no Blog).
Equipe Polimática
Salvador-BA
2013
Classificação dos polígonos:
Lados/Nomes
3: Triângulo
4: Quadrilátero
5: Pentágono
6: Hexágono
7: Heptágono
8: Octógono
9: Eneágono
10: Decágono
11: Hendecágono ou Undecágono
12: Dodecágono
.... .....
Polígonos convexos e não convexos:
Se os ângulos do polígono forem menores que 180º ele será convexo.

Caso tenha um ângulo com medida maior que 180º ele será classificado como não convexo ou côncavo.

Ângulos de um polígono:
A soma dos ângulos internos de qualquer polígono depende do número de lados (n), sendo usada a seguinte expressão para o cálculo: S = (n – 2)*180, onde n o número de lados.
A soma dos ângulos externos de qualquer polígono sempre será 360º, baseando-se no seguinte princípio: quanto maior o número de lados do polígono mais ele se assemelha a uma circunferência (possui giro completo igual a 360º).

Polígono regular e irregular:
Todo polígono regular possui os lados e os ângulos com medidas iguais. Alguns exemplos de polígonos regulares.

Um polígono irregular é aquele que não possui os ângulos com medidas iguais e os lados não possuem o mesmo tamanho.

Diagonais de um polígono:
Diagonal de um polígono é o segmento de reta que liga um vértice ao outro, passando pelo interior da figura. O número de diagonais de um polígono depende do número de lados (n) e pode ser calculado pela expressão:
.jpg)
By: Davi Garrido (Postador no Blog).
Equipe Polimática
Salvador-BA
2013
domingo, 11 de agosto de 2013
Um pouco de poesia...
"A razão é como uma equação
De matemática... tira a prática
De sermos... um pouco mais de nós!"
Fernando Anitelli
De matemática... tira a prática
De sermos... um pouco mais de nós!"
Quadriláteros: Conceitos e Exemplos.
> Em geral, um quadrilátero será uma figura geométrica limitada por quatro lados, todos diferentes e que formam entre si quatro ângulos internos também diferentes. Em qualquer caso, a soma das amplitudes dos ângulos internos de um quadrilátero é sempre 360º.
Quando existe determinada regularidade quanto aos comprimentos e/ou às posições relativas de alguns dos lados do quadrilátero este recebe uma designação especial:
*Trapézio - quadrilátero que tem, pelo menos, dois lados paralelos. A esses lados dá-se o nome de bases do trapézio (base maior e base menor). A distância que separa as duas bases, medida na perpendicular a ambas, designa-se por altura do trapézio;

*Paralelogramo - quadrilátero cujos lados são paralelos dois a dois. Sendo paralelos dois a dois, os lados opostos têm igual comprimento e os ângulos opostos têm a mesma amplitude. Além disso, as diagonais do paralelogramo intersectam-se no ponto médio de cada uma.

*Quadrado - retângulo que tem dois lados consecutivos com o mesmo comprimento (o que implica que todos os lados sejam iguais).

*Losango - paralelogramo em que dois lados consecutivos têm o mesmo comprimento. As diagonais de um losango são perpendiculares entre si.

* Fonte: http://www.infopedia.pt/$quadrilateros;jsessionid=hfHcs3xB3CIl1A3u-HaMZQ
*By: Equipe Polimática.
Salvador-BA
2013.
Quando existe determinada regularidade quanto aos comprimentos e/ou às posições relativas de alguns dos lados do quadrilátero este recebe uma designação especial:
*Trapézio - quadrilátero que tem, pelo menos, dois lados paralelos. A esses lados dá-se o nome de bases do trapézio (base maior e base menor). A distância que separa as duas bases, medida na perpendicular a ambas, designa-se por altura do trapézio;

*Paralelogramo - quadrilátero cujos lados são paralelos dois a dois. Sendo paralelos dois a dois, os lados opostos têm igual comprimento e os ângulos opostos têm a mesma amplitude. Além disso, as diagonais do paralelogramo intersectam-se no ponto médio de cada uma.

*Quadrado - retângulo que tem dois lados consecutivos com o mesmo comprimento (o que implica que todos os lados sejam iguais).

*Losango - paralelogramo em que dois lados consecutivos têm o mesmo comprimento. As diagonais de um losango são perpendiculares entre si.

* Fonte: http://www.infopedia.pt/$quadrilateros;jsessionid=hfHcs3xB3CIl1A3u-HaMZQ
*By: Equipe Polimática.
Salvador-BA
2013.
quarta-feira, 7 de agosto de 2013
terça-feira, 6 de agosto de 2013
Mudança de Rumo!!
Pessoal do clube de matemática, nos administradores do blogger acabamos com a fase de postagens sobre a Matemática no Enem e no Concurso Público, publicamos vídeos, dicas, assuntos que geralmente caem em provas como estas e muito mais. Esperamos ter ajudado bastante e agora a partir de hoje voltaremos a explicar os assuntos normalmente e este blog será atualizado diariamente para melhor ensina-los e visite-nos sempre que puderem..
* By: Davi Garrido (Administrador do blog e postador).
Equipe Polimática.
* By: Davi Garrido (Administrador do blog e postador).
Equipe Polimática.
sábado, 3 de agosto de 2013
quinta-feira, 1 de agosto de 2013
Rumo ao Enem!!!
> Pessoal do Clube, nós administradores do Blog estamos com o objetivo de preparar todos vocês para provas como o Enem, mesmo que o Enem já tenha sido realizado, é sempre bom se preparar antecipadamente para o próximo, então nosso blog durante um certo tempo " sempre " estará publicando sobre assuntos de Matemática que caíram no Enem algumas dicas sobre como realizar a prova, estamos trabalhando ao máximo para que vocês tenham o melhor conteúdo, até lá estaremos qui postando várias aulas e a partir de agora somos 2º professor de matemática de vocês, bons estudos!!!
quarta-feira, 31 de julho de 2013
terça-feira, 30 de julho de 2013
Trigonometria ( Vídeos).
Fonte: Yotube.
By: Equipe Polimática.
Obs: Esta coleção de vídeos serve como suporte estudantil para provas sobre trigonometria.
domingo, 28 de julho de 2013
Veja 10 temas que podem cair na prova de matemática do Enem
1) Álgebra, gráficos e tabelas
Entenda como são pedidos os conteúdos básicos de matemática no exame.
Álgebra é a essência da matemática. Em cima dela é que se resolve as questões. No Enem é julgada a interpretação do texto. É importante tirar as informações que podem vir em forma de equação, gráficos ou tabelas. Analisar gráficos e tabelas é comum nas provas do Enem.
2) Porcentagem
Do financiamento do carro às promoções das lojas, quase tudo o que envolve as contas dos brasileiros traz o sinal de "porcentagem". Ele aparece no juro do empréstimo, na remuneração da poupança, nos preços das ações. Mas muita gente ainda tem dúvidas sobre como fazer as contas.
3) Análise combinatória
Na análise combinatória não interessa quais são as soluções, mas quantas são as soluções. Para questões mais elaboradas, é preciso usar uma das três possibilidades de cálculo: os arranjos, as combinações ou as permutações. A análise combinatória permite saber quantos jogos da Mega-Sena com 15 dezenas é possível fazer.
4) Estatística
Média, moda, mediana, variância e desvio padrão de um conjunto de valores são alguns conceitos de estatística que podem aparecer no Enem.
5) Logarítimo
O logaritmo pode ser aplicado, por exemplo, nas questões que pedem para que sejam comparadas as energias entre dois terremotos e a formação de tsunamis.
6) Geometria plana
Questões sobre geometria plana e geometria espacial são frequentes nas provas do Enem. Veja ao lado um exemplo de como calcular a área de um triângulo quando são conhecidos dois lados e o ângulo entre eles.
7) Geometria espacial
Em geometria espacial, questões sobre cones, cubos, pirâmides e prismas são comuns no Enem. Os prismas são sólidos cujas bases são sempre paralelas e iguais. Há dois tipos de prisma: reto e oblíquo. Entenda como se calcula a área dele.
8) Cálculo
Exemplos práticos como o número de acidentes de trânsito podem ser abordados para que o candidato use cálculo e raciocínio para resolver a questão.
9) Geometria analítica
Questões de geometria analítica podem ser usadas para situações do cotidiano. No exemplo ao lado, veja como o cálculo pode ser feito para determinar quantos litros de cada combustível é necessário comprar para obter a maior autonomia possível de um veículo com motor flex.
10) Interdisciplinariedade
As questões de matemática podem vir em um contexto junto com física, onde no cálculo de forças resultantes é utilizado trigonometria, ou ainda combinada em questões de química, biologia ou geografia, com leitura de gráficos.
*Fonte: G1 Educação.
*By: Equipe Polimática.
Entenda como são pedidos os conteúdos básicos de matemática no exame.
Álgebra é a essência da matemática. Em cima dela é que se resolve as questões. No Enem é julgada a interpretação do texto. É importante tirar as informações que podem vir em forma de equação, gráficos ou tabelas. Analisar gráficos e tabelas é comum nas provas do Enem.
2) Porcentagem
Do financiamento do carro às promoções das lojas, quase tudo o que envolve as contas dos brasileiros traz o sinal de "porcentagem". Ele aparece no juro do empréstimo, na remuneração da poupança, nos preços das ações. Mas muita gente ainda tem dúvidas sobre como fazer as contas.
3) Análise combinatória
Na análise combinatória não interessa quais são as soluções, mas quantas são as soluções. Para questões mais elaboradas, é preciso usar uma das três possibilidades de cálculo: os arranjos, as combinações ou as permutações. A análise combinatória permite saber quantos jogos da Mega-Sena com 15 dezenas é possível fazer.
4) Estatística
Média, moda, mediana, variância e desvio padrão de um conjunto de valores são alguns conceitos de estatística que podem aparecer no Enem.
5) Logarítimo
O logaritmo pode ser aplicado, por exemplo, nas questões que pedem para que sejam comparadas as energias entre dois terremotos e a formação de tsunamis.
6) Geometria plana
Questões sobre geometria plana e geometria espacial são frequentes nas provas do Enem. Veja ao lado um exemplo de como calcular a área de um triângulo quando são conhecidos dois lados e o ângulo entre eles.
7) Geometria espacial
Em geometria espacial, questões sobre cones, cubos, pirâmides e prismas são comuns no Enem. Os prismas são sólidos cujas bases são sempre paralelas e iguais. Há dois tipos de prisma: reto e oblíquo. Entenda como se calcula a área dele.
8) Cálculo
Exemplos práticos como o número de acidentes de trânsito podem ser abordados para que o candidato use cálculo e raciocínio para resolver a questão.
9) Geometria analítica
Questões de geometria analítica podem ser usadas para situações do cotidiano. No exemplo ao lado, veja como o cálculo pode ser feito para determinar quantos litros de cada combustível é necessário comprar para obter a maior autonomia possível de um veículo com motor flex.
10) Interdisciplinariedade
As questões de matemática podem vir em um contexto junto com física, onde no cálculo de forças resultantes é utilizado trigonometria, ou ainda combinada em questões de química, biologia ou geografia, com leitura de gráficos.
*Fonte: G1 Educação.
*By: Equipe Polimática.
sábado, 27 de julho de 2013
Você sabia que...
A arca de Noé têm os seguintes comprimentos: trezentos côvados o comprimento da arca, e de cinquenta côvados a sua largura, e de trinta côvados a sua altura.
Glossário: Côvado significa Medida de comprimento que foi usada por diversas civilizações antigas. Era baseado no comprimento do antebraço, da ponta do dedo médio até o cotovelo.
sexta-feira, 26 de julho de 2013
Logarítimos.
A hipérbole equilátera
> Seja a função real f(x)=1/x definida para todo x diferente de zero. O gráfico desta função é a curva plana denominada hipérbole equilátera, sendo que um ramo da hipérbole está no primeiro quadrante e o outro está localizado no terceiro quadrante.

Esta curva tem importantes aplicações em Ótica e construções de óculos, lentes, telescópios, estudos de química, estudos em economia, etc.
Ln(u)=área(1,u)
e u>1, a região possuirá uma área bem definida, mas tomando u=1, a região se reduzirá a uma linha vertical (que não posssui área ou seja, possui área nula) e neste caso tomaremos Ln(1)=área(1,1). Assim:
Ln(1)=0
Quando aumentamos os valores de u, esta função também aumenta os seus valores, o que significa que esta função é crescente para valores de u>0.
O conceito de Integral de uma função real, normalmente estudado na disciplina Cálculo Diferencial e Integral, justifica a forma como apresentamos o Logaritmo natural de um número real.
Propriedades gerais dos logaritmos
Com o uso deste conceito fundamental da Matemática, é possível demonstrar várias propriedades dos Logaritmos naturais (o que não será feito aqui), para números reais positivos x e y e para qualquer número real k, desde que tenham sentido as expressões matemáticas:
*Propriedades básicas dos logaritmos naturais
- Ln(1)=0
- Ln(x.y)=Ln(x)+Ln(y)
- Ln(xk)=k.Ln(x)
- Ln(x/y)=Ln(x)-Ln(y)
Algumas simplificações matemáticasAs propriedades dos Logaritmos podem ser usadas para simplificar expressões matemáticas.
Exemplos:
- Ln(5)+4.Ln(3)=Ln(5)+Ln(34=Ln(5.34)=Ln(405)
- (1/2)Ln(4t²)-Ln(t)=Ln[(4t²)½]-Ln(t)=Ln(2), se t>0
- Ln(a)+L(b)-Ln(c)+Ln(10)=Ln(10a.b/c)
2 Ln(3) = Ln(3²) = Ln(9)
3 Ln(2) = Ln(2³) = Ln(8)
e como a função Ln é crescente, então:3 Ln(2) = Ln(2³) = Ln(8)
3 Ln(2) = Ln(8)<Ln(9) = 2 Ln(3)
Base para um logaritmo
Existe um importante número real e=2,71828... (atribuído a Euler) tal que
Ln(e) = 1
A partir da observação anterior, o número e representa a base para os logaritmos naturais e poderemos escrever:
Ln(u) = Loge(u)
que lemos como "logaritmo do número real u na base e".A partir do exposto acima, temos uma propriedade que possibilita a mudança logarítmica de uma base positiva para outra base positiva, sendo que ambas devem ser diferentes de 1.
Loga(b) = Ln(b) / Ln(a)
Exercício: Você saberia a razão pela qual não é possível definir logaritmo de um número na base 1?
Logaritmo decimal
No âmbito do Ensino Médio, usa-se bastante a base 10, uma vez
que neste ambiente a base decimal recebe as preferências para o
trabalho com o nosso sistema de numeração, mas devemos
observar que em contextos mais avançados, a base decimal tem pouca
utilidade. Quando escrevermos Log a partir daqui neste trabalho,
entenderemos o Logaritmo na base decimal e escrevemos:
y = Log(x)
para entender que y é o Logaritmo de x na base 10 e nesta base 10,
temos algumas características interessantes com os logaritmos das
potências de 10- Log(1)=0
- Log(0) não tem sentido
- Log(10)=Log(101)=1
- Log(1/10)=Log(10-1)=-1
- Log(100)=Log(10²)=2
- Log(1/100)=Log(10-2)=-2
- Log(1000)=Log(10³)=3
- Log(1/1000)=Log(10-3)=-3
- Log(10n)=n
- Log(10-n)=-n
Log 10n=n
temos que o Logaritmo de 10n na base 10 é o expoente n, o que nos faz pensar que para todo x real positivo vale a relação:
Log(10x) = x
Definição estranha de logaritmo
A última expressão mostrada acima é correta e existe uma outra
relação muito mais geral do que esta, pois o Logaritmo de um número real
positivo x na base b é igual ao número e se, e somente se, x pode ser escrito como a potência b elevada ao expoente e, isto é:
Logb(x) = e se, e somente se, x = be
Em livros de Matemática elementar, esta é tomada como a definição de
Logaritmo de um número em uma certa base, o que é estranho pois tal
definição é cíclica:- Define-se o logarítmo em função da exponencial;
- Define-se a exponencial em função do logaritmo.
Cálculos de logaritmos de alguns números
Com a definição estranha é possível obter o um valor aproximado para o Log(2). Consideremos que y=Log(2) e 10y=2. Inicialmente, temos que Log(2) é positivo e menor do que 1, pois 1<2<10 assim
0<Log(2)<1
É interessante obter dois números que sejam potências de 2 e que estejam muito próximos de potências de 10.Por exemplo:
1000<1024=210
8192=213<10000,
logo 1000<1024<8192<10000, assim, aplicando o logaritmo de base 10, teremos:8192=213<10000,
3<10 Log(2)<13 Log(2)<4
então
0,300=3/10<Log(2)<4/13=0,308
e a média aritmética entre 0,300 e 0,308 é 0,304, que é uma boa estimativa para Log(2), isto é:
Log(2)=0,304
O ideal é encontrar outras potências de 10 que estejam próximas de potências de 2, o que não é fácil para alguém que não
tenha uma calculadora que opere com muitos decimais, o que pode ser visualizado através da tabela mostrando algumas de tais
potências:| Intervalo | Valores | Média |
|---|---|---|
| 1<2 <10 | 0<Log(2)<1 | 0,500 |
| 1<2²<10 | 0<Log(2)<1/2 | 0,250 |
| 10<24<10² | 1/4<Log(2)<2/4 | 0,375 |
| 10<25<10² | 1/5<Log(2)<2/5 | 0,300 |
| 10<26<10² | 1/6<Log(2)<2/6 | 0,250 |
| 10²<28<10³ | 2/8<Log(2)<3/8 | 0,313 |
| 10³<210<104 | 3/10<Log(2)<4/10 | 0,350 |
| 10³<211<104 | 3/11<Log(2)<4/11 | 0,318 |
| 10³<212<104 | 3/12<Log(2)<4/12 | 0,292 |
| 10³<213<104 | 3/13<Log(2)<4/13 | 0,269 |
| 104<214<105 | 4/14<Log(2)<5/14 | 0,321 |
| 104<215<105 | 4/15<Log(2)<5/15 | 0,300 |
| 104<216<105 | 4/16<Log(2)<5/16 | 0,282 |
| 105<217<106 | 5/17<Log(2)<6/17 | 0,393 |
| 105<218<106 | 5/18<Log(2)<6/18 | 0,306 |
| 105<219<106 | 5/19<Log(2)<6/19 | 0,289 |
| 106<220<107 | 6/20<Log(2)<7/20 | 0,325 |
Em Cálculo Diferencial e Integral, podemos desenvolver a função Ln através de uma série de potências de x para calcular logaritmos de números reais positivos com -1<x<1.
Ln(1+x) = x - (1/2) x² + (1/3) x³ - (1/4) x4 + (1/5) x5 + ...
Uma outra série mais eficiente, permite obter o valor de Ln(y) para
qualquer y real desde que se saiba o valor de x para o qual
y=(1+x)/(1-x).
Ln(y) = 2 [ x + (1/3) x³ + (1/5) x5 + (1/7) x7 + ... ]
Por exemplo, para obter Ln(3), tomamos y=3 e deveremos ter x=1/2 para satisfazer à relação y=(1+x)/(1-x).Voltando ao estudo básico, Log(2)=0,3010299956639812... e com este valor, podemos obter os logaritmos das potências de 2, como por exemplo:
- Log(4)=Log(2²)=2Log(2)=0,60206
- Log(8)=Log(2³)=3Log(2)=0,90309
- Log(16)=Log(24)=4Log(2)=1,20412
- Log(32)=Log(25)=5Log(2)=1,50515
- Log(2n)=n.Log(2)
- Log(1/2)=Log(2-1)=(-1)Log(2)=-0,30103
- Log(1/4)=Log(2-2)=(-2)Log(2)=-0,60206
- Log(1/8)=Log(2-3)=(-3)Log(2)=-0,90309
- Log(1/16)=Log(2-4)=(-4)Log(2)=-1,20412
- Log(1/32)=Log(2-5)=(-5)Log(2)=-1,50515
- Log(2-n)=(-n).Log(2)
Com Log(2) e Log3, não é possível calcular os logaritmos dos números primos maiores do que 5, mas é possível obter uma grande quantidade de logaritmos de números naturais.
Exemplo: Usaremos Log(2)=0,301 e Log(3)=0,477, para calcular alguns logaritmos.
- Log(5)=Log(10/2)=Log(10)-Log(2)=1-0,301=0,699
- Log(6)=Log(2.3)=Log(2)+Log(3)=0,301+0,477=0,778
- Log(8)=Log(2³)=3 Log(2)=0,903
- Log(9)=Log(3²)=2 Log(3)=0,954
Log(7)=0,840
Característica e mantissa de um logaritmo na base 10
Se um número está entre duas potências consecutivas de 10, o expoente da menor delas é a característica do logaritmo deste número e a diferença entre o logaritmo do número e a característica é a mantissa que é a parte decimal do logaritmo.
| Número | Logaritmo | Característica | Mantissa |
|---|---|---|---|
| 0,002 | ¯3,30103 | -3 | 0,30103 |
| 0,02 | ¯2,30103 | -2 | 0,30103 |
| 0,2 | ¯1,30103 | -1 | 0,30103 |
| 2 | 0,30103 | 0 | 0,30103 |
| 20 | 1,30103 | 1 | 0,30103 |
| 200 | 2,30103 | 2 | 0,30103 |
| 2000 | 3,30103 | 3 | 0,30103 |
¯3,30103 significa que apenas a característica é negativa, valendo -3 e ela deve ser somada à mantissa que é um número positivo 0,30103 e isto significa que o resultado deve ser um número com um sinal negativo, isto é, -2,69897.
Tábua moderna de logaritmos
Para obter o logaritmo de um número positivo, não se esqueça de colocar o ponto decimal no lugar da vírgula.Exercício: Calcular Log(2), Log(20), Log(200) e Log(2000). Observou algo interessante sobre as características e mantissas desses logaritmos?
Inequação do 2º Grau.
As inequações são expressões matemáticas que utilizam, na sua formatação, os seguintes sinais de desigualdades:
>: maior que
<: menor que
≥: maior ou igual
≤: menor ou igual
≠: diferente
As inequações do 2º grau são resolvidas utilizando o teorema de Bháskara. O resultado deve ser comparado ao sinal da inequação, com o objetivo de formular o conjunto solução.
Exemplo 1
Vamos resolver a inequação 3x² + 10x + 7 < 0.
Exemplo 2
Determine a solução da inequação –2x² – x + 1 ≤ 0.
Exemplo 3
Determine a solução da inequação x² – 4x ≥ 0.
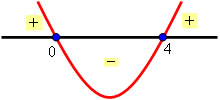
S = {x ? R / x ≤ 0 ou x ≥ 4}
Exemplo 4
Calcule a solução da inequação x² – 6x + 9 > 0.
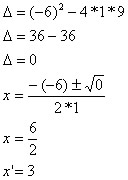
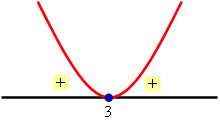
S = {x ? R / x < 3 e x > 3}
>: maior que
<: menor que
≥: maior ou igual
≤: menor ou igual
≠: diferente
As inequações do 2º grau são resolvidas utilizando o teorema de Bháskara. O resultado deve ser comparado ao sinal da inequação, com o objetivo de formular o conjunto solução.
Exemplo 1
Vamos resolver a inequação 3x² + 10x + 7 < 0.
Exemplo 2
Determine a solução da inequação –2x² – x + 1 ≤ 0.
Exemplo 3
Determine a solução da inequação x² – 4x ≥ 0.

S = {x ? R / x ≤ 0 ou x ≥ 4}
Exemplo 4
Calcule a solução da inequação x² – 6x + 9 > 0.
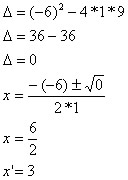

S = {x ? R / x < 3 e x > 3}
Salvador-BA
2013
By: Equipe Polimática.
quinta-feira, 25 de julho de 2013
Os pontos notáveis do triângulo
O incentro
O baricentro

| |||||||||||||
O baricentro
A mediana de um triângulo é o segmento de recta que une um vértice e o ponto médio do lado oposto.
Um triângulo admite três medianas.
As medianas de um triângulo intersectam-se num ponto chamadobaricentro que dista dois terços do vértice da mediana correspondente (Teorema de Ceva).

O baricentro é o centro de gravidade do triângulo. Isto quer dizer que, se suspendermos um triângulo de material homogéneo pelo seu baricentro, ele fica em equilíbrio.
O ortocentro
A altura de um triângulo é o segmento perpendicular compreendido entre o vértice e o lado oposto.
Um triângulo admite três alturas.
As alturas (Ha,Hb e Hc) de um triângulo intersectam-se num ponto H,chamado ortocentro.
| ||
 | ||
O circuncentro
A mediatriz do lado de um triângulo é uma recta perpendicular ao lado no seu ponto Médio.
Se traçarmos as mediatrizes dos três lados de um triângulo, elas intersectam-se num ponto O, chamado circuncentro.
Este ponto está equidistante (à mesma distância) dos três vértices do triângulo e é o centro duma circunferência circunscrita ao mesmo.
 | ||
Homenagem ao Professor Luíz Carlos Pacheco
Nós Administradores do Blogger, fazemos uma homenagem através desta postagem ao nosso querido professor de matemática Luíz Carlos, por ter paciência em nos ensinar e amor a sua profissão, a ideia deste blogger foi dele e nós agradecemos muito por este trabalho, PARABÉNS LUÍZ CARLOS, VC É D++++++++++++++++++++++++++++++++++++++++++++++++
Atenciosamente: Equipe Polimática.
Atenciosamente: Equipe Polimática.
quarta-feira, 24 de julho de 2013
Inequação do 1º Grau
Uma inequação do 1° grau na incógnita x é qualquer expressão do 1° grau que pode ser escrita numa das seguintes formas:
ax + b > 0;
ax + b < 0;
ax + b ≥ 0;
ax + b ≤ 0.
Onde a, b são números reais com a ≠ 0.
Exemplos:
-2x + 7 > 0
x – 10 ≤ 0
2x + 5 ≤ 0
12 – x < 0
Exemplo1: Resolva a inequação -2x + 7 > 0.
Solução:
-2x > -7
Multiplicando por (-1)
2x < 7
x < 7/2
Portanto a solução da inequação é x < 7/2.
Exemplo 2: Resolva a inequação 2x – 6 < 0.
Solução:
2x < 6
x < 6/2
x < 3 Portanto a solução da inequação e x < 3
Pode-se resolver qualquer inequação do 1° grau por meio do estudo do sinal de uma função do 1° grau, com o seguinte procedimento:
1. Iguala-se a expressão ax + b a zero;
2. Localiza-se a raiz no eixo x;
3. Estuda-se o sinal conforme o caso.
Exemplo 1:
-2x + 7 > 0
-2x + 7 = 0
x = 7/2
2x – 6 = 0
x = 3
ax + b < 0;
ax + b ≥ 0;
ax + b ≤ 0.
-2x + 7 > 0
x – 10 ≤ 0
2x + 5 ≤ 0
12 – x < 0
Resolvendo uma inequação de 1° grau
Uma maneira simples de resolver uma equação do 1° grau é isolarmos a incógnita x em um dos membros da igualdade. Observe dois exemplos:Exemplo1: Resolva a inequação -2x + 7 > 0.
Solução:
-2x > -7
Multiplicando por (-1)
2x < 7
x < 7/2
Portanto a solução da inequação é x < 7/2.
Exemplo 2: Resolva a inequação 2x – 6 < 0.
Solução:
2x < 6
x < 6/2
x < 3
1. Iguala-se a expressão ax + b a zero;
2. Localiza-se a raiz no eixo x;
-2x + 7 > 0
-2x + 7 = 0
x = 7/2
Exemplo 2:
2x – 6 < 0
2x – 6 < 0
2x – 6 = 0
x = 3
Salvador-BA.
By: Equipe Polimática.
Coolaborador Principal: Deus.
Professor Adjunto: Luíz Carlos Pacheco.
Faça suas perguntas!!
Gente estou colocando aqui nosso email para que vocês enviem suas mensagens:
polimaticos@gmail.com
Envie suas perguntas que se possível darei á alguns professores para responder a vocês!!
polimaticos@gmail.com
Envie suas perguntas que se possível darei á alguns professores para responder a vocês!!
terça-feira, 23 de julho de 2013
Um pouco de poesia.....
O chá arrefece com o tempo,
As plantas florescem com o tempo,
A Matemática aprende-se com o tempo,
A vida vive-se com o tempo.
O que é que não é função do tempo?
(autor desconhecido)
Com um duplo cone e um serrote
Apolônio mostrou ao mundo
Elipses, hipérboles e parábolas.
Eram formas tão perfeitas,
Que na Matemática
Já tinham uma equação.
A sua beleza e harmonia
Levaram-nos do plano para o espaço
E também de Apolônio ao nosso dia-a-dia.
(autor desconhecido)
By: Aluno Davi Garrido.
Salvador-BA
Casos de Congruência dos Triângulos
Temos que dois triângulos são congruentes:
Quando seus elementos (lados e ângulos) determinam a congruência entre os triângulos.
Quando dois triângulos determinam a congruência entre seus elementos.
Casos de congruência:
1º LAL (lado, ângulo, lado): dois lados congruentes e ângulos formados também congruentes.
2º LLL (lado, lado, lado): três lados congruentes.

Quando seus elementos (lados e ângulos) determinam a congruência entre os triângulos.
Quando dois triângulos determinam a congruência entre seus elementos.
Casos de congruência:
1º LAL (lado, ângulo, lado): dois lados congruentes e ângulos formados também congruentes.
2º LLL (lado, lado, lado): três lados congruentes.

3º ALA (ângulo, lado, ângulo): dois ângulos congruentes e lado entre os ângulos congruente.
4º LAA (lado, ângulo, ângulo): congruência do ângulo adjacente ao lado, e congruência do ângulo oposto ao lado.
Através das definições de congruência de triângulos podemos chegar às propriedades geométricas sem a necessidade de efetuar medidas. A esse método damos o nome de demonstração.
Dizemos que, em todo triângulo isósceles, os ângulos opostos aos lados congruentes são congruentes. Os ângulos da base de um triângulo isósceles são congruentes.
Salvador-BA
By: Aluno Davi Garrido.
segunda-feira, 22 de julho de 2013
Repassando Ângulos
Ângulos e suas definições
Denominamos ângulo a região do plano limitada por duas semirretas de mesma origem. As semirretas recebem o nome de lados do ângulo e a origem delas, de vértice do ângulo.
A unidade usual de medida de ângulo, de acordo com o sistema internacional de medidas, é o grau, representado pelo símbolo º, e seus submúltiplos são o minuto ’ e o segundo ”.
Temos que 1º (grau) equivale a 60’ (minutos) e 1’ equivale a 60”(segundos).
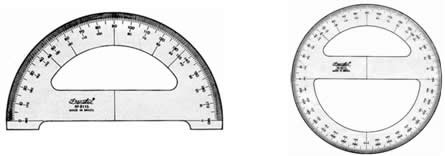
O objeto capaz de medir o valor de um ângulo é chamado de transferidor, podendo ele ser de “meia volta” (180º) ou volta inteira (360º).
Classificação de ângulos
Os ângulos são classificados de acordo com suas medidas:
Agudo: ângulo com medida menor que 90º.
Reto: ângulo com medida igual a 90º.
Obtuso: ângulo com medida maior que 90º.
Raso: ângulo com medida igual a 0º ou 180º.
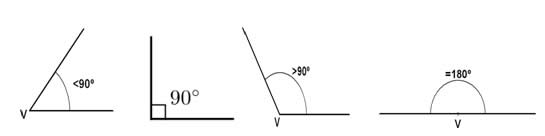
agudo reto obtuso raso
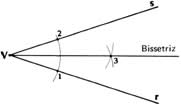
Bissetriz de um ângulo
Bissetriz de um ângulo pode ser definida como a semirreta que se origina no vértice do ângulo principal, dividindo-o em outros dois ângulos com medidas iguais.
Retas paralelas cortadas por uma transversal

Ângulos correspondentes: a e e, d e h, b e f, c e g Congruentes
Ângulos colaterais externos: a e h, b e g Suplementares
Ângulos colaterais internos: e e d, c e f Suplementares
Ângulos alternos externos: a e g, b e h Congruentes
Ângulos alternos internos: d e f, c e e Congruentes
Temos que 1º (grau) equivale a 60’ (minutos) e 1’ equivale a 60”(segundos).
O objeto capaz de medir o valor de um ângulo é chamado de transferidor, podendo ele ser de “meia volta” (180º) ou volta inteira (360º).

Classificação de ângulos
Os ângulos são classificados de acordo com suas medidas:
Agudo: ângulo com medida menor que 90º.
Reto: ângulo com medida igual a 90º.
Obtuso: ângulo com medida maior que 90º.
Raso: ângulo com medida igual a 0º ou 180º.

agudo reto obtuso raso
Bissetriz de um ângulo
Bissetriz de um ângulo pode ser definida como a semirreta que se origina no vértice do ângulo principal, dividindo-o em outros dois ângulos com medidas iguais.

Retas paralelas cortadas por uma transversal

Ângulos correspondentes: a e e, d e h, b e f, c e g Congruentes
Ângulos colaterais externos: a e h, b e g Suplementares
Ângulos colaterais internos: e e d, c e f Suplementares
Ângulos alternos externos: a e g, b e h Congruentes
Ângulos alternos internos: d e f, c e e Congruentes
Assinar:
Postagens (Atom)